Tracing the 2017 Solar Eclipse
-
- Visualizations by:
- Ernie Wright
-
- Edited by:
- Genna Duberstein
-
- Produced by:
- Genna Duberstein
-
- Narration:
- Ernie Wright
- View full credits
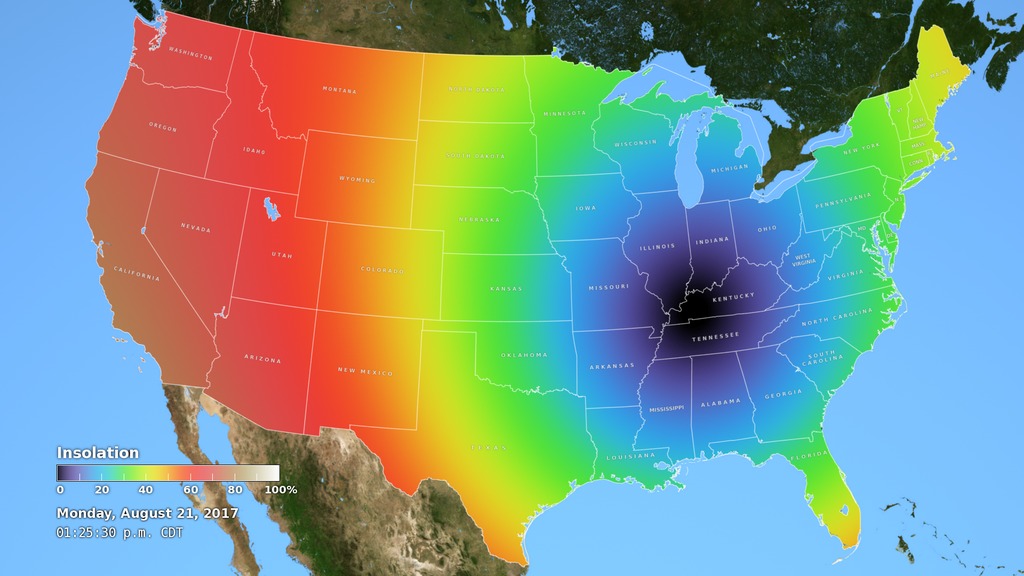
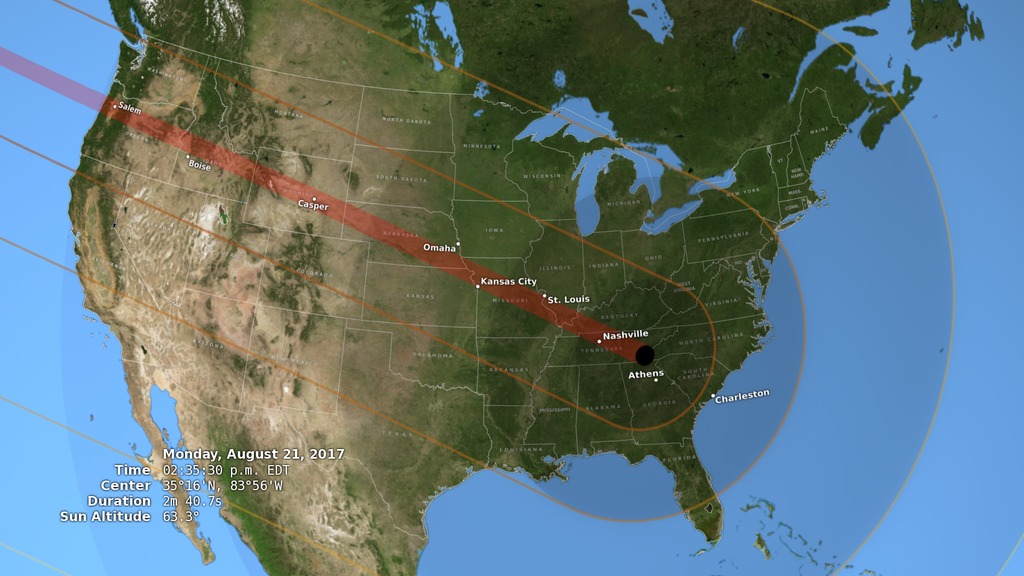
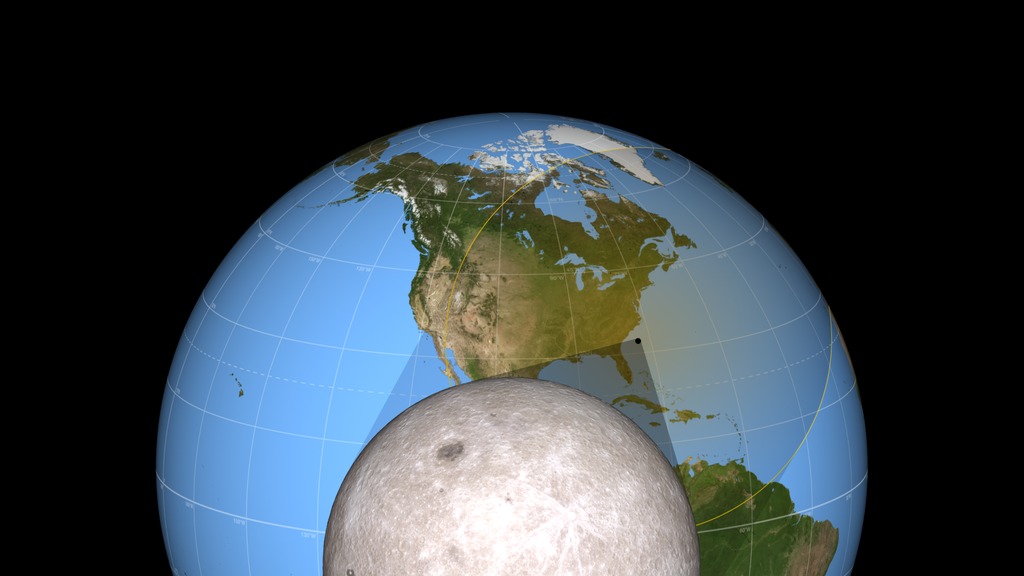
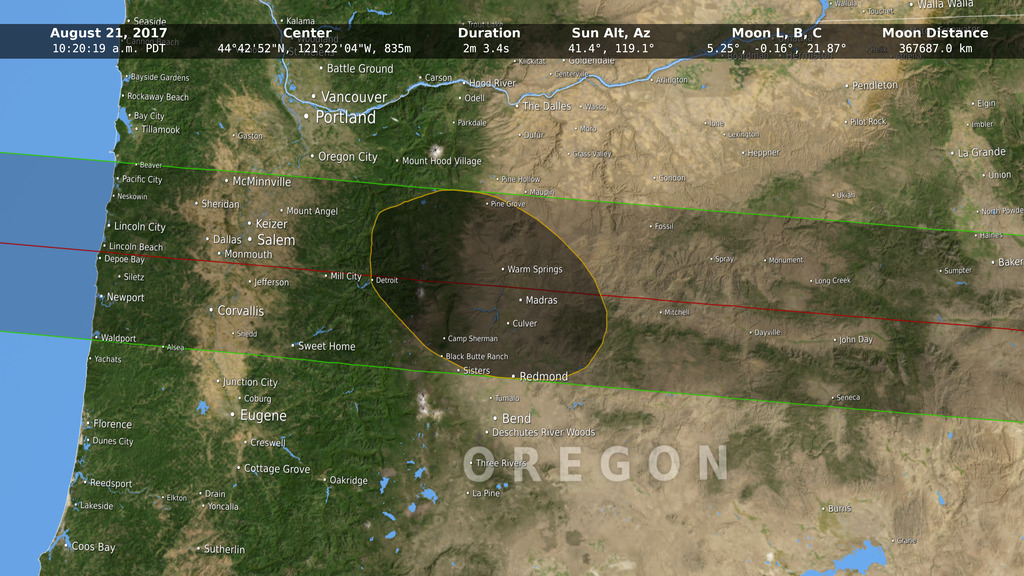
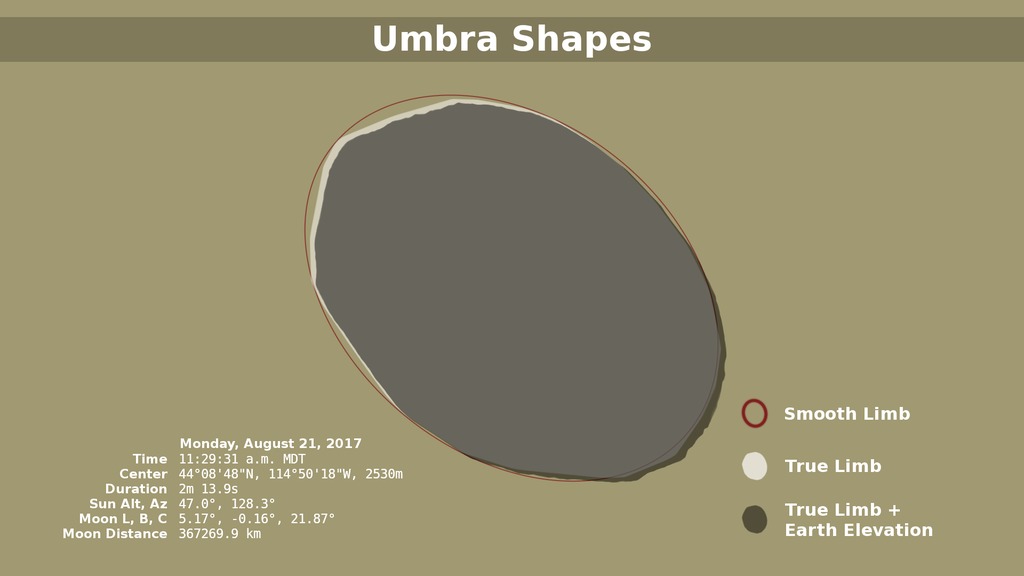
When depicting an eclipse path, data visualizers have usually chosen to represent the moon's shadow as an oval. By bringing in a variety of NASA data sets, visualizer Ernie Wright has created a new and more accurate representation of the eclipse. For the first time, we are able to see that the moon's shadow is better represented as a polygon. This more complicated shape is based NASA's Lunar Reconnaissance Orbiter's view of the mountains and valleys that form the moon's jagged edge. By combining moon's terrain, heights of land forms on Earth, and the angle of the sun, Wright is able to show the eclipse path with the greatest accuracy to date.
Hear data visualizer Ernie Wright discuss the map in the video above. To see the maps unedited, watch the two videos below.
Music credit: Life Choices by Eric Chevalier
Complete transcript available.
Watch this video on the NASA Goddard YouTube channel.
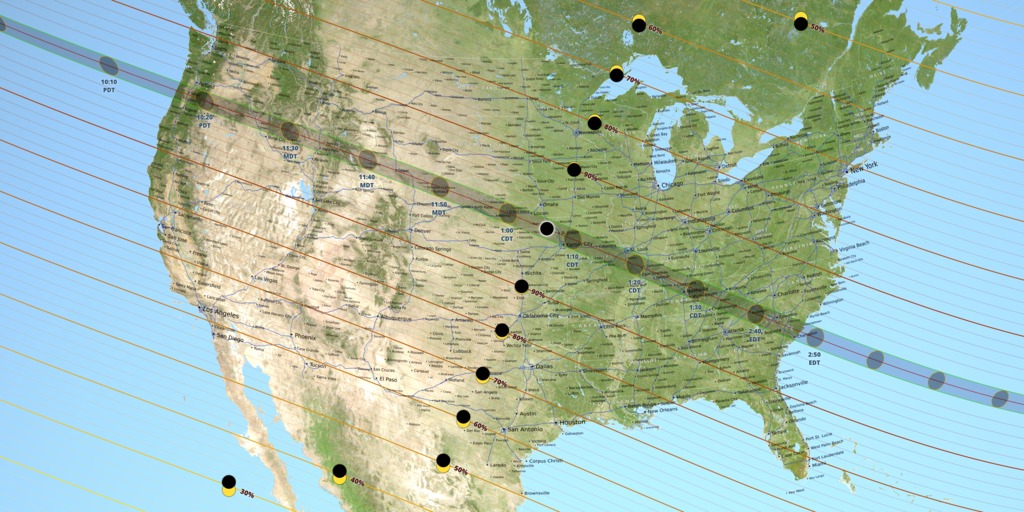
The 2017 Path of Totality Read more about this map
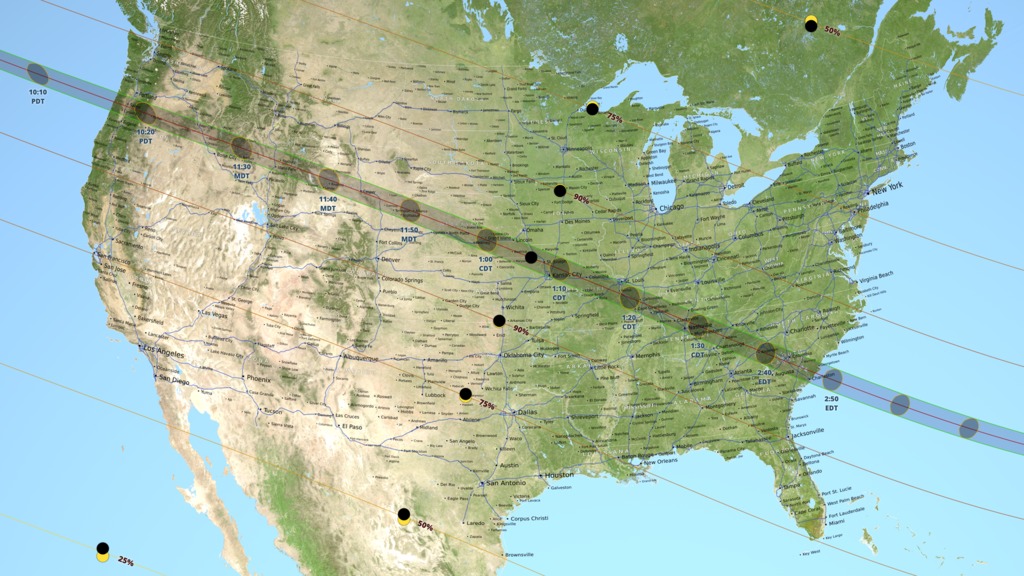
The 2017 Path of Totality: Oblique View Read more about this map
This animation closely follows the Moon's umbra shadow as it passes over the United States during the August 21, 2017 total solar eclipse. Through the use of a number of NASA datasets, notably the global elevation maps from Lunar Reconnaissance Orbiter, the shape and location of the shadow is depicted with unprecedented accuracy.
Credits
Please give credit for this item to:
NASA's Goddard Space Flight Center
-
Visualizer
- Ernie Wright (USRA) [Lead]
-
Editor
- Genna Duberstein (ADNET Systems, Inc.) [Lead]
-
Producer
- Genna Duberstein (ADNET Systems, Inc.) [Lead]
-
Narrator
- Ernie Wright (USRA) [Lead]
Series
This visualization can be found in the following series:Datasets used in this visualization
-
SRTM DEM
ID: 481 -
Terra and Aqua BMNG (Blue Marble: Next Generation)
ID: 508Credit: The Blue Marble data is courtesy of Reto Stockli (NASA/GSFC).
This dataset can be found at: http://earthobservatory.nasa.gov/Newsroom/BlueMarble/
See all pages that use this dataset -
LRO DEM (Digital Elevation Map)
ID: 653 -
DE421 (JPL DE421)
ID: 752Planetary ephemerides
This dataset can be found at: http://ssd.jpl.nasa.gov/?ephemerides#planets
See all pages that use this dataset -
LRO/SELENE SLDEM2015 (DIgital Elevation Model)
ID: 948A digital elevation model of the Moon derived from the Lunar Orbiter Laser Altimeter and the SELENE Terrain Camera. See the description in Icarus. The data is here.
See all pages that use this dataset
Note: While we identify the data sets used in these visualizations, we do not store any further details, nor the data sets themselves on our site.
Related Pages
-
-
ID: 4466 Visualization
Insolation during the 2017 Eclipse
Read moreInsolation (the amount of sunlight reaching the ground) is affected dramatically by the Moon's shadow during the August 21, 2017 total solar eclipse. || usa_insol.0720_print.jpg (1024x576) [123.2 KB] || usa_insol.0720_searchweb.png (320x180) [75.0 KB] || usa_insol.0720_thm.png (80x40) [6.4 KB] || usa_insol_1080p30.mp4 (1920x1080) [17.6 MB] || usa_insol_720p30.mp4 (1280x720) [9.1 MB] || frames/1920x1080_16x9_30p/ (1920x1080) [64.0 KB] || usa_insol_720p30.webm (1280x720) [4.8 MB] || usa_insol_2160p30.mp4 (3840x2160) [53.2 MB] || usa_insol_360p30.mp4 (640x360) [3.1 MB] || frames/3840x2160_16x9_30p/ (3840x2160) [64.0 KB] ||
-
ID: 4390 Visualization
2017 Eclipse: Earth, Moon and Sun
Read moreThe Moon moves right to left in its orbit around the Earth. The shadow it casts hits the Earth during the August 21, 2017 total solar eclipse. || sun_earth.0240_print.jpg (1024x576) [41.2 KB] || sun_earth.0240_searchweb.png (320x180) [37.9 KB] || sun_earth.0240_thm.png (80x40) [3.9 KB] || eclipse2017sunearth_1080p30.mp4 (1920x1080) [3.6 MB] || eclipse2017sunearth_720p30.mp4 (1280x720) [1.6 MB] || frames/1920x1080_16x9_30p/ (1920x1080) [32.0 KB] || eclipse2017sunearth_720p30.webm (1280x720) [2.7 MB] || eclipse2017sunearth_360p30.mp4 (640x360) [514.7 KB] ||
-
ID: 4314 Visualization
2017 Total Solar Eclipse in the U.S.
Read moreA view of the United States during the total solar eclipse of August 21, 2017, showing the umbra (black oval), penumbra (concentric shaded ovals), and path of totality (red) through or very near several major cities. || usa.0780_print.jpg (1024x576) [144.7 KB] || usa.0780_searchweb.png (320x180) [90.1 KB] || usa.0780_thm.png (80x40) [6.8 KB] || eclipse2017usa_1080p30.mp4 (1920x1080) [26.0 MB] || eclipse2017usa_720p30.mp4 (1280x720) [14.0 MB] || eclipse2017usa_720p30.webm (1280x720) [5.0 MB] || frames/1920x1080_16x9_30p/fancy/ (1920x1080) [64.0 KB] || eclipse2017usa_2160p30.mp4 (3840x2160) [69.5 MB] || eclipse2017usa_360p30.mp4 (640x360) [5.1 MB] || frames/3840x2160_16x9_30p/fancy/ (3840x2160) [64.0 KB] || frames/9600x3240_3x1_30p/ (9600x3240) [64.0 KB] || 2017_US_eclipse_4314.pptx [14.6 MB] || 2017_US_eclipse_4314.key [17.1 MB] ||
-
ID: 4321 Visualization
2017 Eclipse Shadow Cones
Read moreThe umbral and penumbral shadow cones travel across the surface of the Earth during the August 21, 2017 total solar eclipse. || cones.0885_print.jpg (1024x576) [79.2 KB] || cones.0885_searchweb.png (320x180) [46.7 KB] || cones.0885_thm.png (80x40) [4.1 KB] || shadow_cones_1080p30.mp4 (1920x1080) [13.9 MB] || shadow_cones_720p30.mp4 (1280x720) [6.9 MB] || shadow_cones_720p30.webm (1280x720) [5.6 MB] || shadow_cones_720p30.wmv (1280x720) [17.9 MB] || frames/1920x1080_16x9_30p/ (1920x1080) [64.0 KB] || shadow_cones_360p30.mp4 (640x360) [2.3 MB] ||
-
-
-
ID: 4515 Visualization
2017 Path of Totality
Read moreThis visualization closely follows the Moon's umbra shadow as it passes over the United States during the August 21, 2017 total solar eclipse. It covers the one hour and 40 minutes between 10:12 am PDT and 2:52 pm EDT. Through the use of a number of NASA datasets, notably the global elevation maps from Lunar Reconnaissance Orbiter, the shape and location of the shadow is depicted with unprecedented accuracy. || usa.0500_print.jpg (1024x576) [257.5 KB] || usa.0500_searchweb.png (320x180) [108.8 KB] || usa.0500_thm.png (80x40) [7.1 KB] || totpath2017_1080p30.mp4 (1920x1080) [190.1 MB] || totpath2017_720p30.mp4 (1280x720) [123.2 MB] || frames/1280x720_16x9_30p/usa/ (1280x720) [256.0 KB] || totpath2017_720p30.webm (1280x720) [22.3 MB] || totpath2017_2160p30.mp4 (3840x2160) [407.4 MB] || totpath2017_360p30.mp4 (640x360) [40.4 MB] || frames/3840x2160_16x9_30p/ (3840x2160) [256.0 KB] || totpath2017_4515.key [125.2 MB] || totpath2017_4515.pptx [124.7 MB] ||
-
ID: 4516 Visualization
2017 Path of Totality: Oblique View
Read moreThis animation closely follows the Moon's umbra shadow as it passes over the United States during the August 21, 2017 total solar eclipse. Through the use of a number of NASA datasets, notably the global elevation maps from Lunar Reconnaissance Orbiter, the shape and location of the shadow is depicted with unprecedented accuracy. || usa_oblique.4044_print.jpg (1024x576) [307.4 KB] || usa_oblique.4044_searchweb.png (320x180) [115.3 KB] || usa_oblique.4044_thm.png (80x40) [6.7 KB] || totpathoblq2017_1080p30.mp4 (1920x1080) [207.3 MB] || totpathoblq2017_720p30.mp4 (1280x720) [117.9 MB] || totpathoblq2017_720p30.webm (1280x720) [22.6 MB] || totpathoblq2017_2160p30.mp4 (3840x2160) [499.6 MB] || totpathoblq2017_360p30.mp4 (640x360) [39.7 MB] || frames/3840x2160_16x9_30p/ (3840x2160) [512.0 KB] || totpathoblq2017_4516.key [120.0 MB] || totpathoblq2017_4516.pptx [119.6 MB] ||
-
ID: 4517 Visualization
Umbra Shapes
Read moreThis animation shows the shape of the Moon's umbral shadow during the August 21, 2017 total solar eclipse, calculated at three different levels of detail. The dark gray is the closest to the true shape. || umbra.0526_print.jpg (1024x576) [40.0 KB] || umbra.0526_searchweb.png (320x180) [19.1 KB] || umbra.0526_thm.png (80x40) [2.8 KB] || umbra_shapes_1080p30.mp4 (1920x1080) [7.3 MB] || umbra_shapes_720p30.mp4 (1280x720) [4.4 MB] || frames/1920x1080_16x9_30p/shapes/ (1920x1080) [128.0 KB] || umbra_shapes_720p30.webm (1280x720) [10.0 MB] || umbra_shapes_360p30.mp4 (640x360) [1.9 MB] ||
-
ID: 4518 Visualization
2017 Total Solar Eclipse Map and Shapefiles
Read moreA map of the United States showing the path of totality for the August 21, 2017 total solar eclipse. This is version 2 of the map, available at both 5400 × 2700 and 10,800 × 5400. || usa_eclipse_map_v2_print.jpg (1024x512) [192.9 KB] || usa_eclipse_map_v2.tif (5400x2700) [26.7 MB] || usa_eclipse_map_v2x2.tif (10800x5400) [85.4 MB] ||
-
-
-
ID: 12458 Produced Video
Shadow of the Eclipse
Read moreSee the most accurate map for Aug 21, 2017's total solar eclipse. || usa_eclipse_map_16x9_1920x1080_1024x576.jpg (1024x576) [212.7 KB] || usa_eclipse_map_16x9_1920x1080_1920x1080.jpg (1920x1080) [700.1 KB] || usa_eclipse_map_16x9_1920x1080_1920x1080_thm.png (80x40) [8.0 KB] || usa_eclipse_map_16x9_1920x1080_1024x576_searchweb.png (320x180) [110.9 KB] || usa_eclipse_map_16x9_1920x1080.tif (1920x1080) [3.9 MB] || usa_eclipse_map_16x9.tif (4800x2700) [21.5 MB] ||
-