Earth
Sun
Planets and Moons
ID: 4314
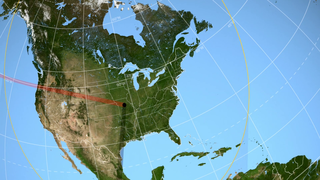
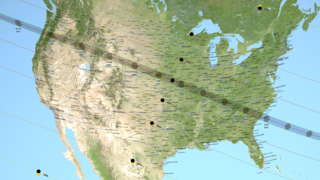
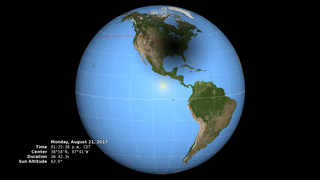
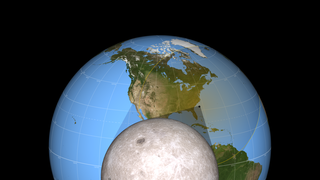
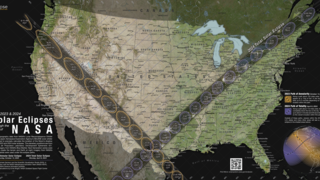
On Monday, August 21, 2017, the Moon will pass in front of the Sun, casting its shadow across all of North America. This will be the first total solar eclipse visible in the contiguous United States in 38 years.
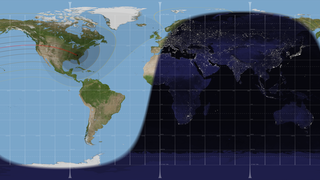
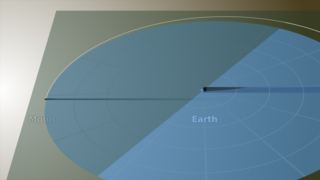
The Moon's shadow can be divided into areas called the umbra and the penumbra. Within the penumbra, the Sun is only partially blocked, and observers experience a partial eclipse. The much smaller umbra lies at the very center of the shadow cone, and anyone there sees the Moon entirely cover the Sun in a total solar eclipse.
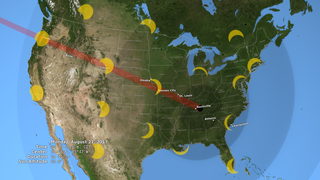
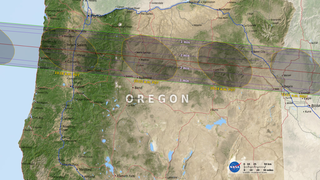
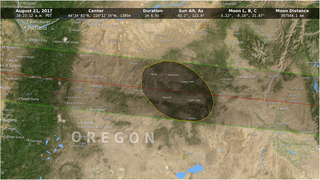
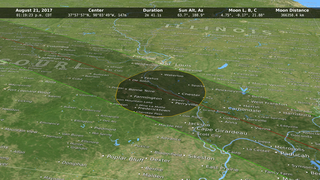
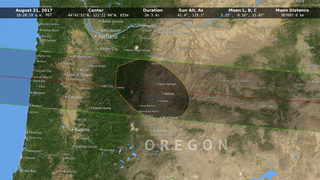
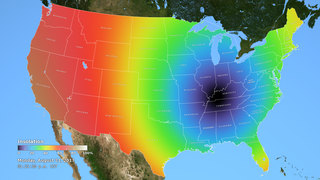
In the animation, the umbra is the small black oval. The red streak behind this oval is the path of totality. Anyone within this path will see a total eclipse when the umbra passes over them. The much larger shaded bullseye pattern represents the penumbra. Steps in the shading denote different percentages of Sun coverage (eclipse magnitude), at levels of 90%, 75%, 50% and 25%. The yellow and orange contours map the path of the penumbra. The outermost yellow contour is the edge of the penumbra path. Outside this limit, no part of the Sun is covered by the Moon.
The numbers in the lower left corner give the latitude and longitude of the center of the umbra as it moves eastward, along with the altitude of the Sun above the horizon at that point. Also shown is the duration of totality: for anyone standing at the center point, this is how long the total solar eclipse will last. Note that the duration varies from just 2 minutes on the West Coast to 2 minutes 40 seconds east of the Mississippi River.
Everyone who performs these calculations will make certain choices to simplify the math or to precisely define an imperfectly known number. The choices often depend on the goals and the computing resources of the calculator, and as you'd expect, the results will differ slightly. You can get quite good results with a relatively simple approach, but it sometimes takes an enormous effort to get only slightly better answers.
The following table lists some of the constants and data used for this animation.
A number of sources explain Bessel’s method of solar eclipse calculation, including chapter 9 of Astronomy on the Personal Computer by Oliver Montenbruck and Thomas Pflager and the eclipses chapter of The Explanatory Supplement to the Astronomical Almanac. The method was adapted to the routines available in NAIF's SPICE software library.
The value for the radius of the Moon is slightly larger than the one used by Fred Espenak and slightly smaller than the one used by the Astronomical Almanac. The Sun radius is the one used most often, but see figure 1 in M. Emilio et al.,
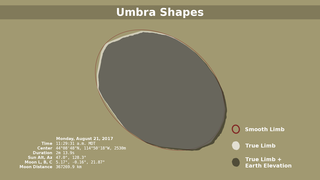
Both the elevations of locations on the Earth and the irregular limb of the Moon were ignored. The resulting small errors mostly affect the totality duration calculation, but they tend to cancel out—elevations above sea level slightly lengthen totality, while valleys along the lunar limb slightly shorten it. The effect on the rendered images is negligible (smaller than a pixel).
Another minor complication that's ignored here is the difference between the Moon's center of mass (the position reported in the ephemeris) and its center of figure (the center of the disk as seen from Earth). These two centers don't exactly coincide because the Moon's mass isn't distributed evenly, but the difference is quite small, about 0.5 kilometers.
2017 Total Solar Eclipse in the U.S.
The Moon's shadow can be divided into areas called the umbra and the penumbra. Within the penumbra, the Sun is only partially blocked, and observers experience a partial eclipse. The much smaller umbra lies at the very center of the shadow cone, and anyone there sees the Moon entirely cover the Sun in a total solar eclipse.
In the animation, the umbra is the small black oval. The red streak behind this oval is the path of totality. Anyone within this path will see a total eclipse when the umbra passes over them. The much larger shaded bullseye pattern represents the penumbra. Steps in the shading denote different percentages of Sun coverage (eclipse magnitude), at levels of 90%, 75%, 50% and 25%. The yellow and orange contours map the path of the penumbra. The outermost yellow contour is the edge of the penumbra path. Outside this limit, no part of the Sun is covered by the Moon.
The numbers in the lower left corner give the latitude and longitude of the center of the umbra as it moves eastward, along with the altitude of the Sun above the horizon at that point. Also shown is the duration of totality: for anyone standing at the center point, this is how long the total solar eclipse will last. Note that the duration varies from just 2 minutes on the West Coast to 2 minutes 40 seconds east of the Mississippi River.
About Accuracy
You might think that calculating the circumstances of an eclipse would be, if not easy, then at least precise. If you do the math correctly, you’d expect to get exactly the same answers as everyone else. But the universe is more subtle than that. The Earth is neither smooth nor perfectly spherical, nor does it rotate at a perfectly constant, predictable speed. The Moon isn’t smooth, either, which means that the shadow it casts isn’t a simple circle. And our knowledge of the size of the Sun is uncertain by a factor of about 0.2%, enough to affect the duration of totality by several seconds.Everyone who performs these calculations will make certain choices to simplify the math or to precisely define an imperfectly known number. The choices often depend on the goals and the computing resources of the calculator, and as you'd expect, the results will differ slightly. You can get quite good results with a relatively simple approach, but it sometimes takes an enormous effort to get only slightly better answers.
The following table lists some of the constants and data used for this animation.
| Earth radius | 6378.137 km |
|---|---|
| Earth flattening | 1 / 298.257 (the WGS 84 ellipsoid) |
| Moon radius | 1737.4 km (k = 0.2723993) |
| Sun radius | 696,000 km (959.634 arcsec at 1 AU) |
| Ephemeris | DE 421 |
| Earth orientation | earth_070425_370426_predict.bpc (ΔT corrected) |
| Delta UTC | 68.184 seconds (TT – TAI + 36 leap seconds) |
A number of sources explain Bessel’s method of solar eclipse calculation, including chapter 9 of Astronomy on the Personal Computer by Oliver Montenbruck and Thomas Pflager and the eclipses chapter of The Explanatory Supplement to the Astronomical Almanac. The method was adapted to the routines available in NAIF's SPICE software library.
The value for the radius of the Moon is slightly larger than the one used by Fred Espenak and slightly smaller than the one used by the Astronomical Almanac. The Sun radius is the one used most often, but see figure 1 in M. Emilio et al.,
Measuring the Solar Radius from Space during the 2003 and 2006 Mercury Transitsfor a sense of the uncertainty in this number.
Both the elevations of locations on the Earth and the irregular limb of the Moon were ignored. The resulting small errors mostly affect the totality duration calculation, but they tend to cancel out—elevations above sea level slightly lengthen totality, while valleys along the lunar limb slightly shorten it. The effect on the rendered images is negligible (smaller than a pixel).
Another minor complication that's ignored here is the difference between the Moon's center of mass (the position reported in the ephemeris) and its center of figure (the center of the disk as seen from Earth). These two centers don't exactly coincide because the Moon's mass isn't distributed evenly, but the difference is quite small, about 0.5 kilometers.
Used Elsewhere In
Alternate Version
Related
Visualization Credits
Ernie Wright (USRA): Lead Visualizer
Tom Bridgman (Global Science and Technology, Inc.): Visualizer
Alex Kekesi (Global Science and Technology, Inc.): Visualizer
Ernie Wright (USRA): Programmer
Genna Duberstein (USRA): Producer
Tom Bridgman (Global Science and Technology, Inc.): Visualizer
Alex Kekesi (Global Science and Technology, Inc.): Visualizer
Ernie Wright (USRA): Programmer
Genna Duberstein (USRA): Producer
Please give credit for this item to:
NASA/Goddard Space Flight Center Scientific Visualization Studio
NASA/Goddard Space Flight Center Scientific Visualization Studio
Short URL to share this page:
https://svs.gsfc.nasa.gov/4314
Data Used:
Note: While we identify the data sets used in these visualizations, we do not store any further details nor the data sets themselves on our site.
This item is part of this series:
2017 Solar Eclipse
Keywords:
SVS >> HDTV
SVS >> Moon
SVS >> Solar Eclipse
SVS >> Hyperwall
SVS >> Eclipse
SVS >> Heliophysics
SVS >> Sun-Earth-Moon Interactions
SVS >> Sun and Earth
NASA Science >> Earth
NASA Science >> Sun
NASA Science >> Planets and Moons
SVS >> Presentation
https://svs.gsfc.nasa.gov/4314
Data Used:
JPL DE421 also referred to as: DE421
Ephemeris - NASA/JPL
Planetary ephemerides
Terra and Aqua/MODIS/Blue Marble: Next Generation also referred to as: BMNG
Credit:
The Blue Marble data is courtesy of Reto Stockli (NASA/GSFC).
The Blue Marble data is courtesy of Reto Stockli (NASA/GSFC).
This item is part of this series:
2017 Solar Eclipse
Keywords:
SVS >> HDTV
SVS >> Moon
SVS >> Solar Eclipse
SVS >> Hyperwall
SVS >> Eclipse
SVS >> Heliophysics
SVS >> Sun-Earth-Moon Interactions
SVS >> Sun and Earth
NASA Science >> Earth
NASA Science >> Sun
NASA Science >> Planets and Moons
SVS >> Presentation